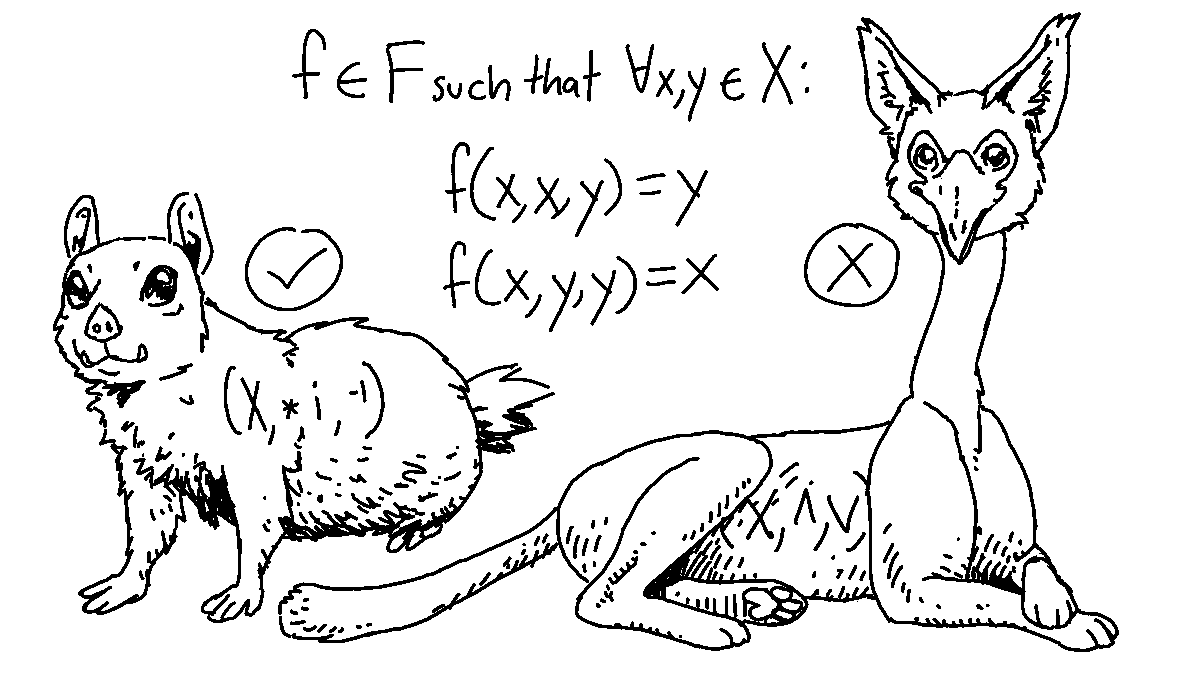ksadov - Malcev Operations

Previously: Algebras

A natural question to ask about any abstract mathematical structure: "is there an interesting way to combine instances of this structure?" Composition is an interesting way to combine congruences on an algebra.

Let R, S be congruences on the algebra (X,F). We compose congruences following the general rule for composing relations: for all x, y, ∈ X, (S∘R)(x,y) iff for some t ∈ X, R(x,t) and S(t,y).

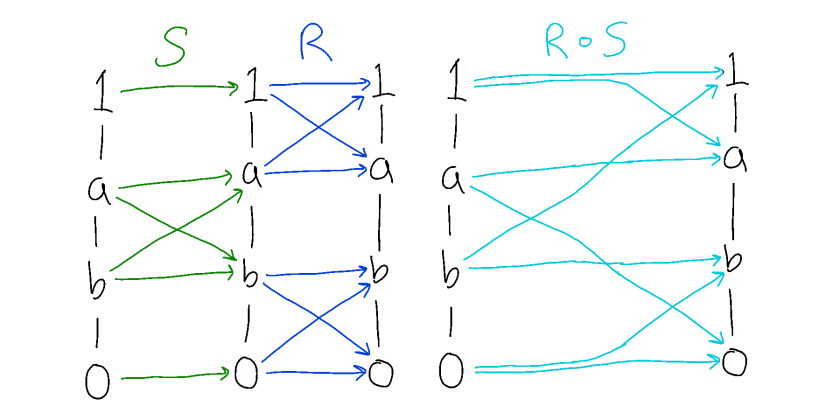
Composing congruences on a lattice ({1,a,b,0},∧,∨)

Composing congruences on the group (ℤ,+,0,−), where "2n" means 2 + ... + 2 with 2 repeated n times, and "3m" means 3 + ... + 3 with 3 repeated m times.

Is the composition of two congruences always a congruence? For groups and rings, the answer is yes. Recall that congruences on a groups correspond to normal subgroups, so that [1]_R = N, [1]_S = M.

[1]_S ∘ R= {g|S ∘ R(1,g)}= {g|∃h such that R(1,h) and S(h,g)}= {g|∃h such that h ∈ N and S(h,g)}= {g|∃h, j such that h ∈ N, j ∈ M and j * h = g} = MN

The product of two normal groups is a normal group, so MN corresponds to a congruence. The proof that composition of congruences on rings corresponds to the product of ideals follows by analogous logic.

The composition of two congruences on a lattice is not always a congruence:

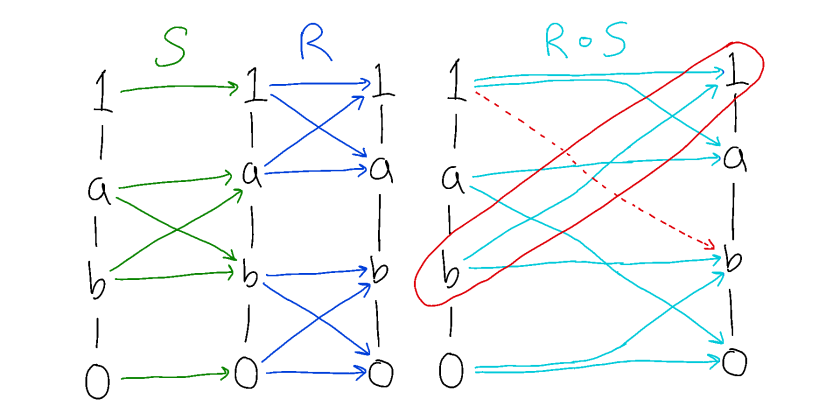
The composition of S and R is not a congruence relation because it isn’t symmetric.

In fact, the composition of congruences is a congruence if and only if the congruences commute.

First assume that congruences commute: for any congruences R, S, on the algebra (X,F), R ∘ S = S ∘ R. Then:

R ∘ S is reflexive: since R and S are congruences, they are reflexive: ∀x ∈ X, S(x,x) and R(x,x). Thus R ∘ S(x,x).
R ∘ S is symmetric: Suppose that we have R ∘ S(x,y). This means that for some t ∈ X, S(x,t) and R(t,y). Since R and S are congruences, they are symmetric, and so S(t,x) and R(y,t). Therefore S ∘ R(x,y), and by our assumption that S ∘ R = R ∘ S, R ∘ S(x,y).
R ∘ S is transitive: Suppose that we have R ∘ S(x,y) and R ∘ S(y,z). Then there exist t, u ∈ X such that S(x,t), R(t,y), S(y,u), R(u,z). From this we can conclude that S ∘ R(t,u), and by our assumption that S ∘ R = R ∘ S, R ∘ S(t,u). This in turn implies that there exists v ∈ X such that S(t,v), R(v,u). Since S, R are congruences and thus transitive, S(x,v) and R(v,z), so R ∘ S(x,z).
R ∘ S preserves operations: Suppose that R ∘ S(x₀,y₀)…R ∘ S(x_n,y_n). Then there exists some t₀…t_n ∈ X such that S(x₀,t₀)…S(x_n,t_n) and R(t₀,y₀)…S(t_n,y_n). Since congruences preserve operations, for any f ∈ F, S(f(x₀…y_n),f(t₀…t_n)) and R(f(t₀…t_n),f(y₀…y_n)). Thus R ∘ S(f(x₀…x_n),f(y₀…y_n)).

Since congruences are reflexive, symmetric, transitive relations that preserve operations, this proves one direction of the proposition. To prove the other direction, begin with the assumption that the composition of congruences is a congruence. Consider the set {(x,y)| such that R ∘ S(x,y)}. By the definition of congruence composition, this is equal to the set {(x,y)| such that ∃t such that S(x,t), R(t,x)}. Since R and S are congruences, they are symmetric relations, and thus this set is equivalent to {(x,y)| such that ∃t such that R(x,t), S(t,x)}, which by definition of congruence equivalence is the set {(x,y)| such that S ∘ R(x,y)}.

Interestingly enough, congruences on an algebra (X,F) are commutative if the algebra contains an operation f ∈ F such that ∀x, y ∈ X, f(x,x,y) = y, f(x,y,y) = x. Such an operation is called a Malcev operation. The group operation f(x,y,z) = x * y⁻¹ * z is a Malcev operation for groups and rings. Lattices in general have no such operation, though specific varieties of lattice may.

When I first learned about Malcev operations, I was surprised that the existence of a single type of operation was enough to make or break congruence commutativity. But the requirement that congruences preserve operations means that operations can place heavy restrictions on which kinds of congruences a structure allows.

Burris and Sankappanavar’s textbook gives a proof that requires building up more terminology than I’d want to include in a blogpost. For the first time in my life, I found a more legible proof on nLab, which also proves some interesting intermediate results. Here it is, rephrased in simpler terms:

Proposition: All congruences on (X,F) commute if F contains a Malcev operation.

(A more general version of the converse proposition also holds, but I won’t get further into it in this post.)

Lemma 1: Given an algebra (X,F), if there exists a Malcev operation f ∈ F, then any reflexive relation R on X that preserves operations is a congruence.

Since congruences are reflexive, transitive, symmetric operations that preserve operations, we just need to show that R is transitive and symmetric. R is transitive because if we have R(x,y) and R(y,z), the fact that R is reflexive gives us R(x,y) ∧ R(y,y) ∧ R(y,z), and then the fact that R preserves operations gives us R(f(x,y,y),f(y,y,z)) = R(x,z). R is symmetric because if we have R(x,y), the reflexivity of R gives us R(x,x) ∧ R(x,y) ∧ R(y,y), and then the fact that R preserves operations gives us R(f(x,x,y),f(x,y,y)) = R(y,x).

Lemma 2: If every reflexive relation R on X that preserves operations is a congruence, then the composition of any two congruences is a congruence.

The composition of two reflexive relations that preserve operations is a reflexive relation that preserves operations, and by hypothesis reflexive relations that preserve operations are congruences.

We’ve already established that the composition of congruences is a congruence if and only if the congruences commute, so these two lemmas show that the existence of a Malcev operation implies that congruences on (X,F) commute.